"We think we have gathered sufficient proof and definitively exclude "hoaxers" in this case. The Bee appeared suddenly at the foot of Milk Hill, in the night from June 25th to June 26th, 2004."
(A "proponent" crop circle website.)
This formation did in no way "appear suddenly", but was discovered by William Betts on June 26, 2004 in a field below Milk Hill, where the chalk White Horse resides since prehistoric times, which English pop amateurs appreciated on the cover of the album English Settlement" by XTC. Each year a number of crop circles are created in this area. This one, as usual, is close to a path, and rather distant from the houses.
The discoverer, William Betts, and some crop circles experts or buffs, say that the circle could not be made by men. For them, it is convincing; you cannot tell exactly who they think created it, but at least they say it is "proved that it was made by men."
The www.cropcirclesecrets.org/crop_circles_history04a.html has a different appreciation:

|
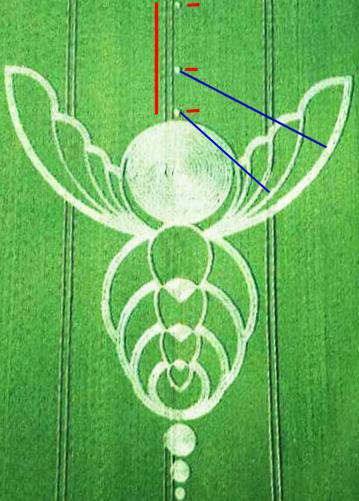
The artists entered the field by "the top" of the image using a tramline.
In red on the image, the tramline they followed, and the very small circles along that tramline, which were used to build the "wings", using a ribbon held by a man at these "holes" with the other end used by the man who flattened the half circles that make the wings. The rays of these half circles are shown in blue.
This is the only reason for the presence of these three "holes" that do not contribute per se to the bee design. The first, useless, was certainly abandoned following a measurement error in the distance with the next.
Some say the design is a winged trilobite, other say it's a bee. In any case, it is hardly a drawing exploit, it is all practically only done with circles countours, full circles and arcs of circles. A true drawing of a bee would be obviously much more difficult to realize, therefore it all simplified to simple geometric patterns so that it is easy to do.
|
Dead flies were found in this formation. This page provides the natural explanation for the dead flies.
The dogma of some proponents of a paranormal or extraterrestrial origin of the crop circles is that the "hoaxed" crop circles have errors while "genuine" crop circles are masterpiece of geometrical perfection, "therefore" impossible to be created by men.
After all, aliens that cannot draw correctly does not seem very serious. It is said that whereas those that have design errors are made by men, those that they claim to be perfectly designed are done by aliens of paranormal powers.
In reality, those claimed to be "genuine" - and we see here that the "genuine" of some "scream hoaxed" for others -, those regarded as genuine do have design errors, which, inter alia, indicates their very human construction. To make a circle is easy, but when there is a lot of circles, and as soon as an opportunity for a mistake exists, the mistake is there. But the "believers" do not see that and/or do not tell about it.
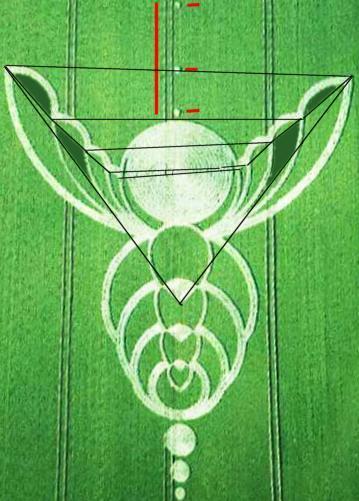
Of course, the circles of the crop circles are beautiful circles. It is rare to make a mistake on this level. Here, the error opportunity relates to the arcs of circle which constitute the wings. Where to start, where to stop when flattening these arcs? There are hardly obvious reference marks to help, and that is why the errors are there, "conveniently", am I tempted to write.
The errors are thus not "anywhere", but where it is logical to expect them, when it is understood that men make these formations and when it is understood that errors are difficult to avoid.
|
I sometimes read that crop circles are made by aliens because it would take "hours" or "days" for "over trained commandos" to do them. It is simply not true and that has been proven many times but "believers" do not want to let you know, or do not know.
Not one investigator seems to have found it useful to publish the dimensions of this formation, which is all the same quite lame and yet usual.
The largest "filled" central circle is obviously flattened by a layout of an external contour then concentric filling until the center is reached or the other way round. On the photograph, one can count approximately 12 of these circles, which suggests a radius of 12 meters if a plank of 1 meter wide is used. By proportion the size of the formation can be estimated as some 100 meters wide.
With 100 meters in width, calculations for its creation give the following numbers:
Using a one meter broad plank, it is thus necessary to make 12 circles of decreasing radii from 12 meters to one meter, that is to say:
12 * 2 * PI = 75
11 * 2 * PI = 69
10 * 2 * PI = 62
9 * 2 * PI = 57
8 * 2 * PI = 50
7 * 2 * PI = 44
6 * 2 * PI = 38
5 * 2 * PI = 31
4 * 2 * PI = 25
3 * 2 * PI = 18
2 * 2 * PI = 13
1 * 2 * PI = 6
- * 2 * PI = 3
This makes out for a distance to flatten of 490 meters.
Three other filled circles are at the "head" of the "bee". Compared with the largest filled circle of 25 meters in diameter, they are respectively of 8 meters, 5 meters and 3 meters diameter approximately.
Their creation thus requires:
4 * 2 * PI = 50
3 * 2 * PI = 18
2 * 2 * PI = 13
1 * 2 * PI = 6
That is 90 meters, generously counted.
3 * 2 * PI = 18
2 * 2 * PI = 13
1 * 2 * PI = 6
That is 40 meters.
2 * 2 * PI = 13
1 * 2 * PI = 6
That is 20 meters.
These three circles filled thus require 150 meters.
5 partial unfilled circles form the veins of the wings. They were traced using a ribbon, the centers from where the man holding one end of the ribbon stood are clearly visible, there is no esthetic reason to them, and they are very conveniently aligned and right beside a tramline (this should be enough to make anyone sensible understand that the formation is made by men, but no investigator made a comment about this).
For the portion of circle forming the external contour of the wings, we have a circle of a broad diameter of 90 meters, generously estimated.
If the circle were complete, we would need two passes since the trace has the width of two planks, therefore a circle of 90 * PI = 282 meters, 282 *2 = 565 meters.
But only half of the circle is flattened, we thus have 282 meters.
The interior edge of the wings is a double layout too, obviously shorter than the external edge, but let's say it is just as long as the external contour, that is to say 282 meters.
The veins of the wings are also half-circles, of less broad layout made in one pass.
They have decreasing diameters respectively of 62, 46, 35 and 28 meters.
That of 62 meters thus has a run of 62 * pi / 2 = 97 meters.
That of 46 meters thus has a run of 46 * PI = 145, 145 / 2 = 73 meters.
That of 35 meters needs 35 * pi = 110 meters, 110 / 2 = 55 meters.
The innermost circle of the veins is 28 meters in diameter and is a complete circle, we thus have: 28 * pi = 88 meters.
The veins thus require 97 + 73 + 55 + 28 meters = 253 meters.
The central part of the bee is formed of 4 complete circles contours made in two passes as their width show. These circles have respective diameters of 39, 30, 23 and 15 meters, hence:
39 * PI * 2 = 245
30 * PI * 2 = 188
23 * PI * 2 = 144
15 * PI * 2 = 94
But these circles are nor complete.
That of 245 meters is less than 2/3, we have 245 * 2 / 3 = 163 meters.
That of 188 meters is less than 2/3, we have 188 * 2 / 3 = 125 meters.
That of 144 meters is less than 2/3, we have 144 * 2 / 3 = 96 meters.
The smallest is not entirely complete, let's not be cheap and keep its 94 meters.
These four circles of the central part require a run of 163 + 125 + 96 + 94 = 478 meters.
In the middle of the central part we still have 4 figures of pointed circles whose largest width are 20, 16, 12 and 6 meters.
By generously comparing these figures to circles, which exaggerates the length, we have:
20 * PI = 63
16 * PI = 50
12 * PI = 38
6 * PI = 19
That is, 170 meters.
For three of these figures, there is a triangle completed with an arc of circle, entirely flattened. Generously, we can consider that this is like squares whose sides are that of a side of the triangular part, like 3 squares of 6, 4 and 2 meters sides, which gives distances to flatten of 36, 16 and 4 meters, that is 68 meters in all.
To create the crop circle of "The Bee" you that need to flatten:
490 + 150 + 282 + 282 + 253 + 478 + 170 + 68 = 2173 meters.
At a low speed of two kilometers per hour, it thus requires little more than 2 hours for one man to flatten all that, with only one other man to hold the ribbon.
This is the most pessimistic option: that of a team of only two people, with only one man for flattening, and with only one board of only 1 meter width.
Although by no means a cereologist, but a ufologist, it hardly took me long to discover that this formation shows the errors of the artists, at the expected places. It shows the evidence of the logic of human construction.
Conversely, no evidence makes it possible to claim that aliens or paranormal forces made this crop circle.
This formation should never have been claimed to be proof that there are "true" crop circles not be made by men.