ALSACAT-1972-05-07-CHALAMPE-1
Mr. P. Rolland told the ufology magazine Lumières Dans La Nuit of January 1973 about a sighting in Chalampé in the Haut-Rhin on May 7, 1972, at 09:00 p.m.
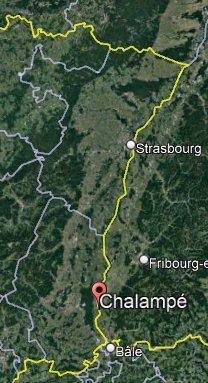
One Mr. R. Patois, 20, and his sister, older, were on flat ground a few hundred meters from the Canal d'Alsace.
There they saw a very bright luminous sphere resembling a lightbulb of yellow-white color.
When they saw it, the object was located to their left, in the 10 clock direction ie northwest. Its altitude was between 600 and 1000 meters, the distance, difficult to estimate, between 2 and 10 km.
The apparent size was that of a fist.
The object was moving relatively slowly, flying in a wide circle several times before taking a north-northeast direction, going up in the cloud layer.
The sighting lasted about 5 minutes.
| Date: | May 7, 1972 |
|---|---|
| Time: | 09:00 p.m. |
| Duration: | ~5 minutes. |
| First known report date: | January 1973 |
| Reporting delay: | 9 months. |
| Department: | Haut-Rhin |
|---|---|
| City: | Chalampé |
| Place: | From a few hundred meters from Canal d'Alsace, UFO in the sky. |
| Latitude: | 47.821 |
| Longitude: | 7.537 |
| Uncertainty radius: | 2 km |
| Number of alleged witnesses: | 2 |
|---|---|
| Number of known witnesses: | 1 or 2 |
| Number of named witnesses: | 1 |
| Witness(es) ages: | 20, >20 |
| Witness(es) types: | A young adult and his older sister. |
| Reporting channel: | Correspondent to ufology magazine LDLN. |
|---|---|
| Type of location: | From flat ground, UFO in the sky. |
| Visibility conditions: | Night. |
| UFO observed: | Yes |
| UFO arrival observed: | ? |
| UFO departure observed: | Yes |
| Entities: | No |
| Photographs: | No. |
| Sketch(s) by witness(es): | No. |
| Sketch(es) approved by witness(es): | No. |
| Witness(es) feelings: | ? |
| Witnesses interpretation: | ? |
| Hynek: | NL |
|---|---|
| ALSACAT: | Possible plane or helicopter. |
[Ref. ld1:] UFOLOGY MAGAZINE "LUMIERES DANS LA NUIT":

|
68) HAUT.RHIN
CHALAMPE
May 7, 1972, at 09:00 p.m.
Mr. R. Patois, 20 years old, and his sister, older, being on a flat place at several hundred meters of the Channel of Alsace (along which the power plant of Fessenheim is located, at 12 km.) saw a luminous sphere looking like a light bulb of very strong yellow-white light. The object moved quite slowly, following several times a large circle before taking a N-NE direction while going up in the cloud layer. The observation lasted 5 minutes approximately. At the time when they saw it, the object was on their left (at 10:00) that is in the NW. The altitude was between 600 and 1000 m., the distance, difficult to evaluate, between 2 and 10 km. The apparent size was that of a fist. (At 14 km. in the NW passes the BAVIC line. Michelin map #66 fold 10. Chalampé is at 14 km. in the NE of Mulhouse).
(Communication by Mr. P. Rolland.)
[Ref. pg1:] MYSELF, PREVIOUSLY:
Mr. R. Patois, aged 20, accompanied by his older sister, were on a flat ground at a few hundreds of meters of the channel of Alsace, close to Chalampé (Rhone-Poulenc and Pec-Rhin chemicals plants, the atomic power plant of Fessenheim is 12 kilometers down along the channel of Alsace.)
At their North-West, they saw a luminous sphere of which they said it resembled an electric bulb, with a very sharp light of white-yellowish color. The sphere moved slowly, went along the same broad circular path several times, then at the end of five minutes of this manoeuver, went up in the clouds layer in direction of the North North-East.
They evaluated the altitude of the sphere as between 600 and 1000 meters, and, noting that the distance appeared difficult to evaluate, estimated it at between 2 and 10 kilometers of them. It should be noted that if the object had been at 14 kilometers of them it would have been located on the famous Bayonne-Vichy line.
[Ref. cvn2:] CHRISTIAN VALENTIN:
Former journalist Christian Valentin published in 2012 a very interesting book telling the story of UFO sightings, flying saucers sightings, in Alsace, from the beginning to 1980.
In this book, he reports that in their Contact Lecteurs number 16 for January 1973, the magazine Lumières dans la Nuit mentioned that on May 7, 1972, at 9 p.m., Mr. R. P. was with his sister at several hundred meters from the Alsace channel at the level of Chalampé when he swa in the Northwest, at an altitude estimated between 600 et 1000 meters and a distance from 2 to 10 km, a luminous sphere of very bright yellow white color resembling an electric light bulb.
On a duration of about 5 minutes, the object slowly performed several large circles in the sky before rising to the cloud layer in the direction of the North/North-Est.
|
The Fessenheim nuclear power plant is not 12 km of Chalampé but only 8 km. Some ufologists associate, not always with reason, UFOs and nuclear power plants if there is a nuclear power plants at a certain proximity of the place of observation.
Here, we are told that the thing was northwest at 2 to 10 kilometers of the witnesses initially; it was not at the nuclear plant which is in the north, but in the direction of Bantzenheim (~ 2 km), Rumersheim-le-Haut (~ 4 km) or Munchhouse (~ 8 km). Taking a north-northeast direction, it could have come close of the nuclear plant - all depends on the viewing distance and its hardly possible assessment, given as 2 to 10 km.
The magazine also noted: "A 14 km in the NW passes BAVIC". The so-called "BAVIC-line" (for Bayonne - Vichy), is an imaginary line noted by Aimé Michel in 1954 and subsequent years as being the place of an unusually high number of UFO sightings. But a gap that could be of 12 kilometers would have been reason enough for Aimé Michel not to count this observation as havging taken place with certainty on that line.
Chalampé is located next to the Canal d'Alsace, the witnesses are said to have been "a few hundred meters" of the Canal, so they might probably have been at the Western limits of Chalampé.
The observation has low strangeness. The maneuver performed could have been that of a helicopter, an airplane, a jet fighter. It was apparently the intensity of the light that could have been the cause of the puzzlement of the witnesses, but unfortunately this intensity was not quantified.
Possible plane or helicopter.
* = Source is available to me.
? = Source I am told about but could not get so far. Help needed.
| Main author: | Patrick Gross |
|---|---|
| Contributors: | None |
| Reviewers: | None |
| Editeur: | Patrick Gross |
| Version: | Create/changed by: | Date: | Description: |
|---|---|---|---|
| 0.1 | Patrick Gross | July 17, 2015 | Creation, [ld1], [pg1], [cvn2]. |
| 1.0 | Patrick Gross | July 17, 2015 | First published. |